- Get access to programs.
- Bands for Si and Gallium Arsenide. See lecture notes.
- Changes in GaAs bands lattice constant.
Answer: NOTE ENERGY SCALE IS EV FOR GRAPHS HEREOur calculations give the gap at k=0 to be: a = 10.6769569, Egap = 9.13899 - 7.95793 = 1.181 eV a = 10.5769569, Egap = 9.69436 - 8.42144 = 1.273 eV Thus V(dEgap/dV) = -.09/.03 = -3. compared to the experimental value of -10.
- Distort the lattice in two ways as listed below. In each case you should
find that bands shift and certain degenerate states split.
- Distort the lattice with no change in volume by compressing along the x
axis by 1% and expanding along y and z by 0.5%. Experimentally it is found
that the highest occupied bands split by delta E = 3b(exx - eyy - ezz) where
exx is the fractional change in the x length, etc., and the value of b is
around -2.0 eV.
Answer:Our calculations give delta E = XX or b = (Not finished)
- Displace the two atoms in the unit cell along the 111 axis by changing
the value of the internal parameter from .125 to a different value. Do the
answers make sense? Do states split as expected?
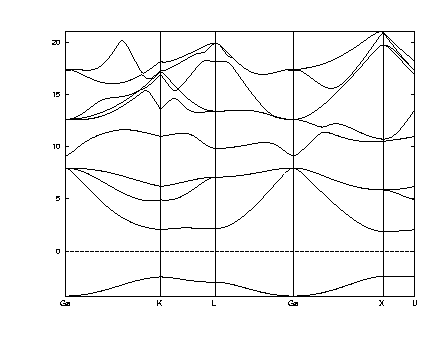
Answer:postscript figure of bands for GaAs with atoms displaced to +- .12,.12,.12
The results in the figure for .125 changed to .12 (i.e. .125 - delta/2) show that the bands at the top of the valence bands split. This is the splitting due to the fact that the crystal is not cubic. The one band that goes down is has weight centered on the bond that gets stronger (shorter); the two that go up are linear combinations of the three bonds that get weaker (longer).
The splitting is around delta E ~ 0.7eV or delta E/delta ~ 7eV.
- Distort the lattice with no change in volume by compressing along the x
axis by 1% and expanding along y and z by 0.5%. Experimentally it is found
that the highest occupied bands split by delta E = 3b(exx - eyy - ezz) where
exx is the fractional change in the x length, etc., and the value of b is
around -2.0 eV.
- Carry out a calculation for metallic hydrogen at a high density which is
thought to exist in the heavy planets like Jupiter. (Think about the problem
yourself, but an input file input file h1.dat is provided that will run the
calculation for the following case.)
Choose an fcc crystal with one atom per primitive cell and a density so that the electron density parameter in atomic units is 1.0 (This corresponds to a pressure around 10 Mbar.) For the potential choose the Coulomb potential screened by an approximate dielectric function for a homogeneous gas with density rs = 1, i.e., V(q) = (4pi/vol)(1/q**2)/epsilon(q), where epsilon(q) = 1. + (k0/q)**2, with k0 the Thomas-Fermi wavevector k0 = 0.815 kFermi sqrt(rs) = 1.56/sqrt(rs) (in atomic units: m=hbar=e=1). See Ashcroft and Mermin, p. 342. Plot the bands just as for Si or GaAs since this is also an fcc crystal. Is hydrogen nearly-free-electron-like at this density? Qualitatively, where is the Fermi energy? Can you estimate it from your calculations?
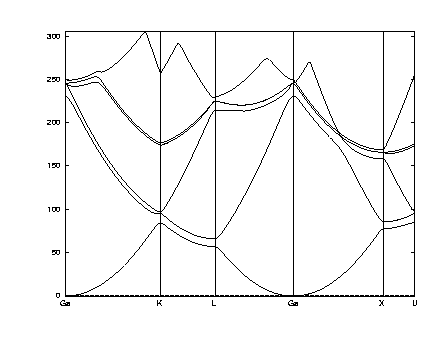
Answer:For an fcc crystal with rs = 1, a = cube edge is given by a^3/4 = (4pi/3)rs^3, or a = (16pi/3)^(1/3) rs = 2.559 rs In potential, we need: The volume per primitive cell is (4pi/3)rs^3 ko^2 = 2.95^2 (a0/rs) /Ang^2 = (.529 * 2.95)^2/rs in a.u. = 2.43/rs in a.u. (Ashcroft and Mermin, p. 342) Thus the potential Fourier components for q2=q^2 is: V(q2) = (4pi/vol)/(q2 + k0^2) = (3/rs^3)/(q2 + 2.43/rs) The bands can be plotted using the same points as for GaAs. The Fermi energy is near the value given by Aschroft and Mermin, EF = 50.1eV/(rs**2) = 50.1 eV in this case, corresponding to the first band being half filled.
postscript figure of bands for H at rs=1 with the screened potential - The bands calculated with the CG method agree to a much greater accuracy than can be seen on the graph. However, there can be problems in some cases where convegence is hard - so care is needed!
- To show the effects of preconditioning do calculations for the k=0 point for Si using the two files given below. The preconditioning is the form suggested by Teter, et al. accelerates the calculations by about a factor of two in this case. Note that one band converges worse than the rest. This band is in the unoccupied states, but sometimes convergence problems are also found in the lower states.
Return to Richard Martin's Lecture Materials
R. M. Martin (rmartin@uiuc.edu) D. Das (ddas@students.uiuc.edu)